Bayesian statistics, first conceived by the Reverend Thomas Bayes in the 1740s, is at least partly responsible for several significant historical achievements. Bayesian statistics helped Alan Turing crack the Enigma cipher used by the Germans in World War II, aided researchers at Harvard in identifying the authors of the Federalist Papers, allowed the US Navy to locate Soviet submarines, and played a key role in the rise of artificial intelligence. Yet Bayes never envisioned the many applications of his idea. In fact, Bayes most likely came up with the theory named after him in order to disprove philosopher and skeptic David Hume’s argument against the resurrection.
This explanation seems likely because Bayes’ work, which he never published, was discovered after his death by his fellow minister and mathematician friend and colleague Richard Price. Price used Bayes’ theorem to argue that the existence of multiple independent witnesses to a miracle could overcome the improbability of the miracle happening and establish it as a fact. In this article we will take a brief tour of Bayes’ theorem, explore how the inventor of the analytical engine (one of the first computers!) used Bayesian thinking to counter Hume’s argument against the resurrection, and consider the role Bayesian statistics can play in Christian apologetics today.
What Is Bayes’ Theorem? Bayesian statistics is often used to update prior beliefs after observing new data. How well do our existing beliefs explain the relevant data and do we need to update our beliefs? As an example, let’s consider the likelihood that Thomas Bayes wrote his essay on probability to refute David Hume, given that Richard Price used Bayes’ theorem for that very purpose. In this case, our “prior” belief is that Bayes wrote his essay to refute Hume, which we’ll assign a probability of 60%. Why? If 60% seems a bit arbitrary, that’s because it is and this fact drives a school of statisticians called frequentists crazy—but keep in mind that real life often requires making decisions in the face of uncertainty. Also, Bayes was known for engaging in intellectual debate and was devout in his faith.
Now, our data in this case is that Price, a friend of Bayes, used Bayes’ theorem to refute Hume. If Bayes himself had this purpose in mind, it is even more likely that Price, given their friendship, would do so. Thus, we’ll assign the probability of our data about our belief to 80%. Now the tricky part. What is the likelihood that Price would use Bayes’ theorem to refute Hume even if Bayes never intended it for that purpose? This is the probability of the data—whether or not our belief is true—and is necessary to calculate the probability of our belief given the data (see the equation below).
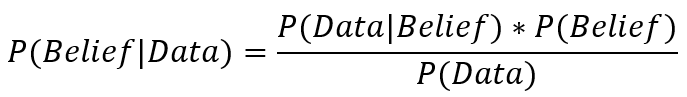
In this case, we’ll say that the probability of Price using Bayes’ theorem to refute Hume— regardless of Bayes’ intent—is reasonably high, since Price himself was eager to engage in such debates. We’ll set the probability of the data regardless of our belief at 65%. We can then calculate, based on our assumptions, the probability of our belief that Bayes wrote his essay to refute Hume.
Now, if we change our assumption and decide that we have no idea how likely Price would be to use Bayes’ theorem to refute Hume on his own, the probability Bayes wrote his essay to refute Hume jumps to 96% because the denominator in our equation changes from .65 to .5, giving us (0.8 * 0.6) / 0.5 = 96%. The point is that Bayes’ equation can give different answers depending on how sure you are that a particular observation could have occurred without the effect you are checking. For example, it’s not likely that a sunny day would give you a stomach ache, but sour milk definitely could. So, this is how you would calculate the probability of a stomach ache given a sunny day:
I’ll leave it to you to calculate this on your own. If you get stuck, just ask ChatGPT or Gemini and they can help you out. In real life there are cases where we can use historical data to know these probabilities more precisely, such as figuring out if a positive cancer test really means you have cancer, which is a very practical application of Bayesian statistics.
Babbage’s Refutation of Hume Let us fast forward from Bayes in the 1740s to Charles Babbage, professor of mathematics at Cambridge and designer of a steam-powered programmable computer called the analytical engine, in the early 1800s. Babbage rephrased Hume’s challenge to eyewitness testimony of miracles (such as the resurrection) as, “The falsehood of testimony of the miracle must be more improbable than the miracle,”1 or as an equation:
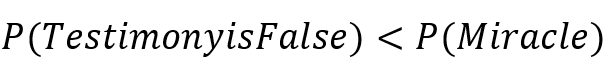
In common vernacular, Hume would only believe claims of the miraculous if the probability that the witnesses were wrong was less than the probability of the miracle, which would be difficult if you assume miracles have a very low probability of occurring. If we assume mutually independent witnesses who are reliable 99% of the time, then the probability of N (number) such witnesses being wrong is given by the following equation:
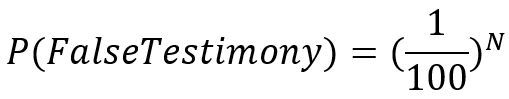
After crunching some numbers using Bayesian equations provided by Pierre-Simon Laplace (the scholar who came up with the mathematical equation for Bayes’ theorem after rediscovering the same principle around 1774), Babbage came to the conclusion that as long as your witnesses speak truth more often than falsehood, there will always be a number of witnesses who can satisfy Hume’s criteria (see Taylor’s paper2 for details). In other words, eyewitness testimony could mathematically provide reasonable evidence for a miraculous event, given certain assumptions about the eyewitnesses.
So What? Bayes’ theorem does not offer “proof” of the miraculous, but it does help us understand how our assumptions impact our beliefs. Hume assumed the probability of the resurrection occurring was zero (weighting the scales just a tiny bit), whereas Babbage calculated it to be 5 * 10-12. By assigning the resurrection a nonzero probability, Babbage made it possible for eyewitness testimony (assuming certain properties of eyewitnesses) to function as reliable evidence for the resurrection (if it’s zero then no amount of evidence would be sufficient). While neither of these numbers may be the “correct” number, they at least allow us to ask fun, meaningful questions, such as “How many eyewitnesses should be necessary for me to accept the resurrection as a historical event based only on the data available to me?”
Ultimately, Bayes’ theorem helps us think about how prior assumptions influence our conclusions when we update our beliefs given a set of facts. Making our priors clear helps us have better apologetic conversations because we understand precisely where we are starting and, when engaging skeptics such as Hume, how to communicate in a way that may open doors for more meaningful dialogue.3
For a scholarly book that considers the probability of God’s existence, see Richard Swinburne, The Existence of God, 2nd ed. (Oxford, UK: Oxford University Press, 2004).
Physicists at CERN’s Large Hadron Collider (LHC) have reported new results showing that the “Higgs-like” boson discovered in 2012 is indeed consistent with expectations...
In the presentation speech for the 1960 Nobel Prize in Chemistry, one scientist described the work by honoree Willard Libby with these words: “Seldom...
